 login/create account
login/create account
Recent Activity
Discrete Logarithm Problem ★★★
Author(s):
If 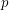 is prime and
is prime and 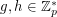 , we write
, we write 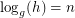 if
if 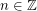 satisfies
satisfies 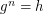 . The problem of finding such an integer
. The problem of finding such an integer  for a given
for a given 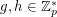 (with
(with 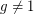 ) is the Discrete Log Problem.
) is the Discrete Log Problem.
Keywords: discrete log; NP
Good Edge Labelings ★★
Author(s): Araújo; Cohen; Giroire; Havet
We say that a graph is good-edge-labeling critical, if it has no good edge labeling, but every proper subgraph has a good edge labeling.
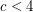 , there is only a finite number of good-edge-labeling critical graphs with average degree less than
, there is only a finite number of good-edge-labeling critical graphs with average degree less than  .
. Keywords: good edge labeling, edge labeling
Special Primes ★
Author(s): George BALAN
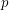 be a prime natural number. Find all primes
be a prime natural number. Find all primes 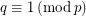 , such that
, such that 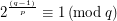 .
.
Keywords:
Three-chromatic (0,2)-graphs ★★
Author(s): Payan
Keywords:
Choice Number of k-Chromatic Graphs of Bounded Order ★★
Author(s): Noel
 is a
is a  -chromatic graph on at most
-chromatic graph on at most 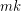 vertices, then
vertices, then 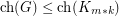 .
. Keywords: choosability; complete multipartite graph; list coloring
The Riemann Hypothesis ★★★★
Author(s): Riemann
The zeroes of the Riemann zeta function that are inside the Critical Strip (i.e. the vertical strip of the complex plane where the real part of the complex variable is in ]0;1[), are actually located on the Critical line ( the vertical line of the complex plane with real part equal to 1/2)
Keywords: Millenium Problems; zeta
Euler-Mascheroni constant ★★★
Author(s):
Keywords: constant; Euler; irrational; Mascheroni; rational; transcendental
Graham's conjecture on tree reconstruction ★★
Author(s): Graham
 , we let
, we let 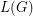 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 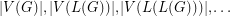 ?
? Keywords: reconstruction; tree
Vertex Cover Integrality Gap ★★
Author(s): Atserias
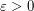 there is
there is 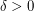 such that, for every large
such that, for every large  , there are
, there are  -vertex graphs
-vertex graphs  and
and  such that
such that  and
and 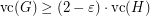 .
. Keywords: counting quantifiers; FMT12-LesHouches
Big Line or Big Clique in Planar Point Sets ★★
Let 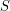 be a set of points in the plane. Two points
be a set of points in the plane. Two points  and
and  in
in 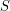 are visible with respect to
are visible with respect to 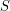 if the line segment between
if the line segment between  and
and  contains no other point in
contains no other point in 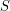 .
.
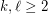 there is an integer
there is an integer  such that every set of at least
such that every set of at least  points in the plane contains at least
points in the plane contains at least 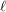 collinear points or
collinear points or  pairwise visible points.
pairwise visible points. Keywords: Discrete Geometry; Geometric Ramsey Theory
Mixing Circular Colourings ★
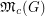 always rational?
always rational? Keywords: discrete homotopy; graph colourings; mixing
The Borodin-Kostochka Conjecture ★★
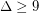 has chromatic number at most
has chromatic number at most 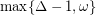 .
. Keywords:
Chromatic number of random lifts of complete graphs ★★
Author(s): Amit
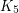 concentrated on a single value?
concentrated on a single value? Keywords: random lifts, coloring
3 is a primitive root modulo primes of the form 16 q^4 + 1, where q>3 is prime ★★
Author(s):
Keywords:
Circular choosability of planar graphs ★
Author(s): Mohar
Let  be a graph. If
be a graph. If 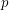 and
and 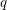 are two integers, a
are two integers, a  -colouring of
-colouring of  is a function
is a function  from
from 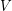 to
to 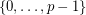 such that
such that  for each edge
for each edge  . Given a list assignment
. Given a list assignment  of
of  , i.e.~a mapping that assigns to every vertex
, i.e.~a mapping that assigns to every vertex  a set of non-negative integers, an
a set of non-negative integers, an  -colouring of
-colouring of  is a mapping
is a mapping  such that
such that  for every
for every 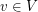 . A list assignment
. A list assignment  is a
is a 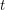 -
- -list-assignment if
-list-assignment if 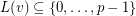 and
and  for each vertex
for each vertex  . Given such a list assignment
. Given such a list assignment  , the graph G is
, the graph G is  -
- -colourable if there exists a
-colourable if there exists a  -
- -colouring
-colouring  , i.e.
, i.e.  is both a
is both a  -colouring and an
-colouring and an  -colouring. For any real number
-colouring. For any real number  , the graph
, the graph  is
is 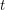 -
- -choosable if it is
-choosable if it is  -
- -colourable for every
-colourable for every 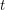 -
- -list-assignment
-list-assignment  . Last,
. Last,  is circularly
is circularly 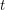 -choosable if it is
-choosable if it is 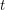 -
- -choosable for any
-choosable for any 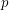 ,
, 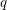 . The circular choosability (or circular list chromatic number or circular choice number) of G is
. The circular choosability (or circular list chromatic number or circular choice number) of G is 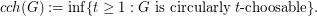
Keywords: choosability; circular colouring; planar graphs
A conjecture about direct product of funcoids ★★
Author(s): Porton
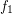 and
and 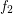 are monovalued, entirely defined funcoids with
are monovalued, entirely defined funcoids with 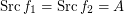 . Then there exists a pointfree funcoid
. Then there exists a pointfree funcoid 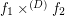 such that (for every filter
such that (for every filter  on
on  )
) 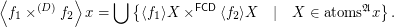 (The join operation is taken on the lattice of filters with reversed order.)
(The join operation is taken on the lattice of filters with reversed order.) A positive solution of this problem may open a way to prove that some funcoids-related categories are cartesian closed.
Keywords: category theory; general topology
MacEachen Conjecture ★
Author(s): McEachen
Keywords: primality; prime distribution
Criterion for boundedness of power series ★
Author(s): Rüdinger
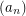 so that the power series
so that the power series 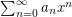 is bounded for all
is bounded for all 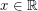 .
. Keywords: boundedness; power series; real analysis
Length of surreal product ★
Author(s): Gonshor
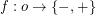 , where
, where  is some ordinal. This
is some ordinal. This  is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of
is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of  as
as 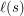 .
.
It is easy to prove that
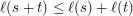
What about
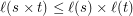
?
Keywords: surreal numbers

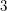 is a
is a 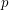 for all primes
for all primes 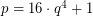 , where
, where 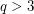 is prime.
is prime.  Drupal
Drupal CSI of Charles University
CSI of Charles University