 login/create account
login/create account
eigenvalues
The sum of the two largest eigenvalues ★★
Author(s): Gernert
Problem Let  be a graph on
be a graph on  vertices and let
vertices and let 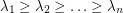 be the eigenvalues of
be the eigenvalues of  . Is
. Is 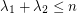 ?
?
 be a graph on
be a graph on  vertices and let
vertices and let 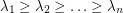 be the eigenvalues of
be the eigenvalues of  . Is
. Is 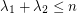 ?
? Keywords: eigenvalues; spectrum
Alon-Saks-Seymour Conjecture ★★★
Author(s): Alon; Saks; Seymour
Conjecture If  is a simple graph which can be written as an union of
is a simple graph which can be written as an union of  edge-disjoint complete bipartite graphs, then
edge-disjoint complete bipartite graphs, then 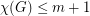 .
.
 is a simple graph which can be written as an union of
is a simple graph which can be written as an union of  edge-disjoint complete bipartite graphs, then
edge-disjoint complete bipartite graphs, then 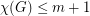 .
. Keywords: coloring; complete bipartite graph; eigenvalues; interlacing
Fowler's Conjecture on eigenvalues of (3,6)-polyhedra ★★
Author(s): Fowler
Conjecture Let  be the graph of a
be the graph of a 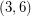 -polyhedron with
-polyhedron with 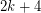 vertices. Then the eigenvalues of
vertices. Then the eigenvalues of  can be partitioned into three classes:
can be partitioned into three classes: 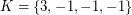 ,
, 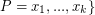 (where
(where 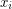 is nonnegative for
is nonnegative for 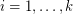 ), and
), and 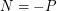 .
.
 be the graph of a
be the graph of a 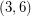 -polyhedron with
-polyhedron with 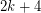 vertices. Then the eigenvalues of
vertices. Then the eigenvalues of  can be partitioned into three classes:
can be partitioned into three classes: 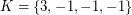 ,
, 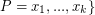 (where
(where 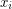 is nonnegative for
is nonnegative for 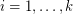 ), and
), and 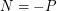 .
. Keywords: (3,6)-polyhedron; eigenvalues

 Drupal
Drupal CSI of Charles University
CSI of Charles University