 login/create account
login/create account
partition
Dividing up the unrestricted partitions ★★
Begin with the generating function for unrestricted partitions:
(1+x+x^2+...)(1+x^2+x^4+...)(1+x^3+x^6+...)...
Now change some of the plus signs to minus signs. The resulting series will have coefficients congruent, mod 2, to the coefficients of the generating series for unrestricted partitions. I conjecture that the signs may be chosen such that all the coefficients of the series are either 1, -1, or zero.
Keywords: congruence properties; partition
Friendly partitions ★★
Author(s): DeVos
A friendly partition of a graph is a partition of the vertices into two sets so that every vertex has at least as many neighbours in its own class as in the other.
 , all but finitely many
, all but finitely many  -regular graphs have friendly partitions?
-regular graphs have friendly partitions? Unfriendly partitions ★★★
If  is a graph, we say that a partition of
is a graph, we say that a partition of 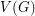 is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.
is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.
Keywords: coloring; infinite graph; partition
Aharoni-Berger conjecture ★★★
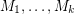 are matroids on
are matroids on 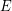 and
and 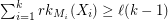 for every partition
for every partition  of
of 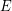 , then there exists
, then there exists 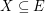 with
with 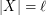 which is independent in every
which is independent in every 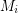 .
. Keywords: independent set; matroid; partition
Bounded colorings for planar graphs ★★
Author(s): Alon; Ding; Oporowski; Vertigan
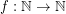 so that every planar graph of maximum degree
so that every planar graph of maximum degree 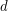 has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets 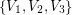 so that for
so that for 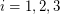 , every component of the graph induced by
, every component of the graph induced by 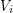 has size at most
has size at most 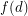 ?
? Keywords: coloring; partition; planar graph
Linial-Berge path partition duality ★★★
 -norm of a path partition on a directed graph
-norm of a path partition on a directed graph 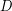 is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph. Keywords: coloring; directed path; partition

 Drupal
Drupal CSI of Charles University
CSI of Charles University