Home » Keyword index

coloring


Graph Theory » Basic G.T. » Minors

Seagull problem ★★★

Author(s): Seymour

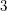Conjecture   Every $ n $ vertex graph with no independent set of size $ 3 $ has a complete graph on 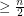$ \ge \frac{n}{2} $ vertices as a minor.

Keywords: coloring; complete graph; minor

Posted by mdevos
updated January 6th, 2008
add new comment
Graph Theory » Coloring » Vertex coloring

Coloring squares of hypercubes ★★

Author(s): Wan

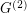If $ G $ is a simple graph, we let $ G^{(2)} $ denote the simple graph with vertex set 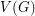$ V(G) $ and two vertices adjacent if they are distance 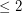$ \le 2 $ in $ G $.

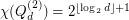Conjecture   $ \chi(Q_d^{(2)}) = 2^{ \lfloor \log_2 d \rfloor + 1} $.

Keywords: coloring; hypercube

Posted by mdevos
updated December 10th, 2008
1 comment
Graph Theory » Infinite Graphs

Unfriendly partitions ★★★

Author(s): Cowan; Emerson

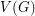If $ G $ is a graph, we say that a partition of $ V(G) $ is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.

Problem   Does every countably infinite graph have an unfriendly partition into two sets?

Keywords: coloring; infinite graph; partition

Posted by mdevos
updated October 22nd, 2007
add new comment
Graph Theory » Topological G.T. » Coloring

5-coloring graphs with small crossing & clique numbers ★★

Author(s): Oporowski; Zhao

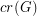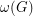For a graph $ G $, we let $ cr(G) $ denote the crossing number of $ G $, and we let $ \omega(G) $ denote the size of the largest complete subgraph of $ G $.

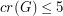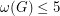Question   Does every graph $ G $ with $ cr(G) \le 5 $ and $ \omega(G) \le 5 $ have a 5-coloring?

Keywords: coloring; crossing number; planar graph

Posted by mdevos
updated October 9th, 2007
add new comment
Graph Theory » Coloring » Vertex coloring

Coloring the Odd Distance Graph ★★★

Author(s): Rosenfeld

The Odd Distance Graph, denoted 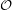$ {\mathcal O} $, is the graph with vertex set 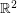$ {\mathbb R}^2 $ and two points adjacent if the distance between them is an odd integer.

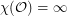Question   Is $ \chi({\mathcal O}) = \infty $?

Keywords: coloring; geometric graph; odd distance

Posted by mdevos
updated March 19th, 2012
8 comments
Graph Theory » Coloring » Vertex coloring

Coloring and immersion ★★★

Author(s): Abu-Khzam; Langston

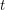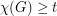Conjecture   For every positive integer $ t $, every (loopless) graph $ G $ with $ \chi(G) \ge t $ immerses $ K_t $.

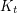Keywords: coloring; complete graph; immersion

Posted by mdevos
updated September 4th, 2007
add new comment
Graph Theory » Coloring » Vertex coloring

Bounding the chromatic number of graphs with no odd hole ★★★

Author(s): Gyarfas

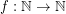Conjecture   There exists a fixed function $ f : {\mathbb N} \rightarrow {\mathbb N} $ so that 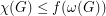$ \chi(G) \le f(\omega(G)) $ for every graph $ G $ with no odd hole.

Keywords: chi-bounded; coloring; induced subgraph; odd hole; perfect graph

Posted by mdevos
updated June 25th, 2007
add new comment
Graph Theory » Topological G.T. » Coloring

5-local-tensions ★★

Author(s): DeVos

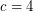Conjecture   There exists a fixed constant $ c $ (probably $ c=4 $ suffices) so that every embedded (loopless) graph with edge-width 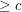$ \ge c $ has a 5-local-tension.

Keywords: coloring; surface; tension

Posted by mdevos
updated June 22nd, 2007
add new comment
Graph Theory » Coloring » Vertex coloring

Alon-Saks-Seymour Conjecture ★★★

Author(s): Alon; Saks; Seymour

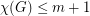Conjecture   If $ G $ is a simple graph which can be written as an union of $ m $ edge-disjoint complete bipartite graphs, then $ \chi(G) \le m+1 $.

Keywords: coloring; complete bipartite graph; eigenvalues; interlacing

Posted by mdevos
updated February 26th, 2010
1 comment
Graph Theory » Topological G.T. » Coloring

Bounded colorings for planar graphs ★★

Author(s): Alon; Ding; Oporowski; Vertigan

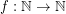Question   Does there exists a fixed function $ f : {\mathbb N} \rightarrow {\mathbb N} $ so that every planar graph of maximum degree 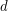$ d $ has a partition of its vertex set into at most three sets 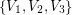$ \{V_1,V_2,V_3\} $ so that for 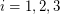$ i=1,2,3 $, every component of the graph induced by 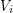$ V_i $ has size at most $ f(d) $?

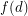Keywords: coloring; partition; planar graph

Posted by mdevos
updated May 23rd, 2007
add new comment
Syndicate content