 login/create account
login/create account
Recent Activity
Seymour's self-minor conjecture ★★★
Author(s): Seymour
Keywords: infinite graph; minor
Perfect 2-error-correcting codes over arbitrary finite alphabets. ★★
Author(s):
Keywords: 2-error-correcting; code; existence; perfect; perfect code
Are there an infinite number of lucky primes? ★
Author(s): Lazarus: Gardiner: Metropolis; Ulam
Something like Picard for 1-forms ★★
Author(s): Elsner
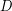 be the open unit disk in the complex plane and let
be the open unit disk in the complex plane and let 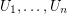 be open sets such that
be open sets such that 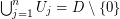 . Suppose there are injective holomorphic functions
. Suppose there are injective holomorphic functions 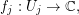
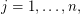 such that for the differentials we have
such that for the differentials we have 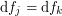 on any intersection
on any intersection 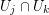 . Then those differentials glue together to a meromorphic 1-form on
. Then those differentials glue together to a meromorphic 1-form on 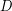 .
. Keywords: Essential singularity; Holomorphic functions; Picard's theorem; Residue of 1-form; Riemann surfaces
The robustness of the tensor product ★★★
Author(s): Ben-Sasson; Sudan
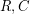 , their Tensor Product
, their Tensor Product 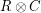 is the code that consists of the matrices whose rows are codewords of
is the code that consists of the matrices whose rows are codewords of 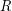 and whose columns are codewords of
and whose columns are codewords of 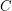 . The product
. The product 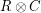 is said to be robust if whenever a matrix
is said to be robust if whenever a matrix 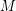 is far from
is far from 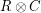 , the rows (columns) of
, the rows (columns) of 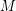 are far from
are far from 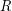 (
(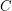 , respectively).
, respectively).
The problem is to give a characterization of the pairs 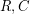 whose tensor product is robust.
whose tensor product is robust.
Keywords: codes; coding; locally testable; robustness
Schanuel's Conjecture ★★★★
Author(s): Schanuel
 complex numbers
complex numbers 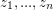 which are linearly independent over the rational numbers
which are linearly independent over the rational numbers 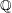 , then the extension field
, then the extension field 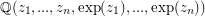 has transcendence degree of at least
has transcendence degree of at least  over
over 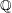 .
. Keywords: algebraic independence
Beneš Conjecture ★★★
Author(s): Beneš
Let 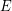 be a non-empty finite set. Given a partition
be a non-empty finite set. Given a partition 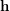 of
of 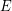 , the stabilizer of
, the stabilizer of 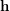 , denoted
, denoted 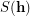 , is the group formed by all permutations of
, is the group formed by all permutations of 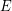 preserving each block of
preserving each block of 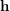 .
.
 ) Find a sufficient condition for a sequence of partitions
) Find a sufficient condition for a sequence of partitions 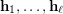 of
of 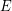 to be complete, i.e. such that the product of their stabilizers
to be complete, i.e. such that the product of their stabilizers 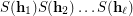 is equal to the whole symmetric group
is equal to the whole symmetric group 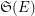 on
on 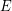 . In particular, what about completeness of the sequence
. In particular, what about completeness of the sequence 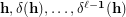 , given a partition
, given a partition 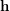 of
of 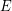 and a permutation
and a permutation  of
of  ?
? 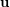 be a uniform partition of
be a uniform partition of 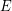 and
and 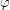 be a permutation of
be a permutation of 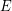 such that
such that 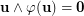 . Suppose that the set
. Suppose that the set 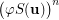 is transitive, for some integer
is transitive, for some integer 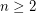 . Then
. Then 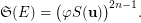
Keywords:
Frankl's union-closed sets conjecture ★★
Author(s): Frankl
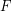 be a finite family of finite sets, not all empty, that is closed under taking unions. Then there exists
be a finite family of finite sets, not all empty, that is closed under taking unions. Then there exists  such that
such that  is an element of at least half the members of
is an element of at least half the members of 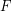 .
. Keywords:
Double-critical graph conjecture ★★
A connected simple graph  is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
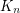 is the only
is the only  -chromatic double-critical graph
-chromatic double-critical graph Keywords: coloring; complete graph
Shuffle-Exchange Conjecture ★★★
Author(s): Beneš; Folklore; Stone
Given integers 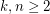 , let
, let 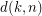 be the smallest integer
be the smallest integer  such that the symmetric group
such that the symmetric group 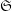 on the set of all words of length
on the set of all words of length  over a
over a  -letter alphabet can be generated as
-letter alphabet can be generated as 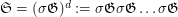 (
(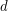 times), where
times), where 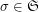 is the shuffle permutation defined by
is the shuffle permutation defined by 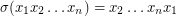 , and
, and 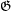 is the exchange group consisting of all permutations in
is the exchange group consisting of all permutations in 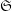 preserving the first
preserving the first 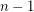 letters in the words.
letters in the words.
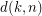 .
. 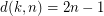 , for all
, for all 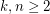 .
. Keywords:
Strong colorability ★★★
Author(s): Aharoni; Alon; Haxell
Let  be a positive integer. We say that a graph
be a positive integer. We say that a graph  is strongly
is strongly  -colorable if for every partition of the vertices to sets of size at most
-colorable if for every partition of the vertices to sets of size at most  there is a proper
there is a proper  -coloring of
-coloring of  in which the vertices in each set of the partition have distinct colors.
in which the vertices in each set of the partition have distinct colors.
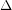 is the maximal degree of a graph
is the maximal degree of a graph  , then
, then  is strongly
is strongly 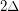 -colorable.
-colorable. Keywords: strong coloring
Is there an algorithm to determine if a triangulated 4-manifold is combinatorially equivalent to the 4-sphere? ★★★
Author(s): Novikov
What is the homotopy type of the group of diffeomorphisms of the 4-sphere? ★★★★
Author(s): Smale
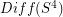 has the homotopy-type of a product space
has the homotopy-type of a product space 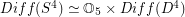 where
where 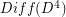 is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of
is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of 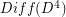 .
. Keywords: 4-sphere; diffeomorphisms
Which compact boundaryless 3-manifolds embed smoothly in the 4-sphere? ★★★
Author(s): Kirby
Keywords: 3-manifold; 4-sphere; embedding
Fundamental group torsion for subsets of Euclidean 3-space ★★
Author(s): Ancient/folklore
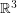 such that its fundamental group has an element of finite order?
such that its fundamental group has an element of finite order?
Keywords: subsets of euclidean space; torsion
Which homology 3-spheres bound homology 4-balls? ★★★★
Author(s): Ancient/folklore
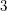 -spheres bound (rational) homology
-spheres bound (rational) homology 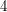 -balls?
-balls?
Keywords: cobordism; homology ball; homology sphere
Realisation problem for the space of knots in the 3-sphere ★★
Author(s): Budney
 in
in 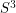 , let the symmetry group of
, let the symmetry group of  be denoted
be denoted 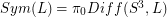 ie: isotopy classes of diffeomorphisms of
ie: isotopy classes of diffeomorphisms of 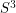 which preserve
which preserve  , where the isotopies are also required to preserve
, where the isotopies are also required to preserve  .
.
Now let  be a hyperbolic link. Assume
be a hyperbolic link. Assume  has the further `Brunnian' property that there exists a component
has the further `Brunnian' property that there exists a component 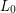 of
of  such that
such that  is the unlink. Let
is the unlink. Let 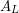 be the subgroup of
be the subgroup of 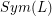 consisting of diffeomorphisms of
consisting of diffeomorphisms of 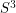 which preserve
which preserve 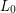 together with its orientation, and which preserve the orientation of
together with its orientation, and which preserve the orientation of 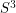 .
.
There is a representation 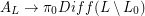 given by restricting the diffeomorphism to the
given by restricting the diffeomorphism to the  . It's known that
. It's known that 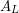 is always a cyclic group. And
is always a cyclic group. And 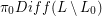 is a signed symmetric group -- the wreath product of a symmetric group with
is a signed symmetric group -- the wreath product of a symmetric group with 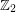 .
.
Problem: What representations can be obtained?
Keywords: knot space; symmetry
Slice-ribbon problem ★★★★
Author(s): Fox
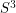 which is slice, is it a ribbon knot?
which is slice, is it a ribbon knot?
Smooth 4-dimensional Schoenflies problem ★★★★
Author(s): Alexander
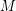 be a
be a 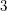 -dimensional smooth submanifold of
-dimensional smooth submanifold of 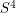 ,
, 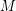 diffeomorphic to
diffeomorphic to 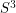 . By the Jordan-Brouwer separation theorem,
. By the Jordan-Brouwer separation theorem, 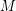 separates
separates 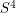 into the union of two compact connected
into the union of two compact connected 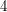 -manifolds which share
-manifolds which share 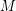 as a common boundary. The Schoenflies problem asks, are these
as a common boundary. The Schoenflies problem asks, are these 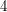 -manifolds diffeomorphic to
-manifolds diffeomorphic to 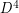 ? ie: is
? ie: is 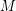 unknotted?
unknotted? Keywords: 4-dimensional; Schoenflies; sphere
Are different notions of the crossing number the same? ★★★
 ?
? ![\[ \text{pair-cr}(G) = \text{cr}(G) \]](/files/tex/8cece1e00bb0e9fc122e0a5cad0dab2681cf33a4.png)
The crossing number 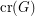 of a graph
of a graph  is the minimum number of edge crossings in any drawing of
is the minimum number of edge crossings in any drawing of  in the plane. In the pairwise crossing number
in the plane. In the pairwise crossing number 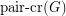 , we minimize the number of pairs of edges that cross.
, we minimize the number of pairs of edges that cross.
Keywords: crossing number; pair-crossing number

 Drupal
Drupal CSI of Charles University
CSI of Charles University