 login/create account
login/create account
Recent Activity
Shuffle-Exchange Conjecture (graph-theoretic form) ★★★
Author(s): Beneš; Folklore; Stone
Given integers 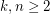 , the 2-stage Shuffle-Exchange graph/network, denoted
, the 2-stage Shuffle-Exchange graph/network, denoted 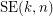 , is the simple
, is the simple  -regular bipartite graph with the ordered pair
-regular bipartite graph with the ordered pair 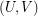 of linearly labeled parts
of linearly labeled parts 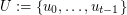 and
and 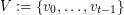 , where
, where 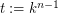 , such that vertices
, such that vertices 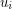 and
and 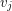 are adjacent if and only if
are adjacent if and only if  (see Fig.1).
(see Fig.1).
Given integers 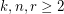 , the
, the  -stage Shuffle-Exchange graph/network, denoted
-stage Shuffle-Exchange graph/network, denoted 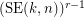 , is the proper (i.e., respecting all the orders) concatenation of
, is the proper (i.e., respecting all the orders) concatenation of 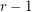 identical copies of
identical copies of 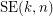 (see Fig.1).
(see Fig.1).
Let 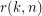 be the smallest integer
be the smallest integer 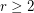 such that the graph
such that the graph 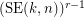 is rearrangeable.
is rearrangeable.
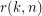 .
. 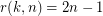 .
. Keywords:
Edge-Colouring Geometric Complete Graphs ★★
Author(s): Hurtado
 vertices has an edge colouring such that:
vertices has an edge colouring such that:- \item[Variant A] crossing edges get distinct colours, \item[Variant B] disjoint edges get distinct colours, \item[Variant C] non-disjoint edges get distinct colours, \item[Variant D] non-crossing edges get distinct colours.
Keywords: geometric complete graph, colouring
Number of Cliques in Minor-Closed Classes ★★
Author(s): Wood
 such that every
such that every  -vertex
-vertex 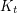 -minor-free graph has at most
-minor-free graph has at most 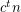 cliques?
cliques? A gold-grabbing game ★★
Author(s): Rosenfeld
Setup Fix a tree 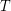 and for every vertex
and for every vertex 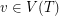 a non-negative integer
a non-negative integer 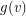 which we think of as the amount of gold at
which we think of as the amount of gold at  .
.
2-Player game Players alternate turns. On each turn, a player chooses a leaf vertex  of the tree, takes the gold at this vertex, and then deletes
of the tree, takes the gold at this vertex, and then deletes  . The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
. The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
Circular colouring the orthogonality graph ★★
Author(s): DeVos; Ghebleh; Goddyn; Mohar; Naserasr
Let 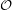 denote the graph with vertex set consisting of all lines through the origin in
denote the graph with vertex set consisting of all lines through the origin in 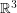 and two vertices adjacent in
and two vertices adjacent in 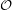 if they are perpendicular.
if they are perpendicular.
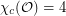 ?
? Keywords: circular coloring; geometric graph; orthogonality
Crossing numbers and coloring ★★★
Author(s): Albertson
We let 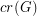 denote the crossing number of a graph
denote the crossing number of a graph  .
.
 with
with 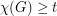 satisfies
satisfies 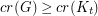 .
. Keywords: coloring; complete graph; crossing number
Domination in cubic graphs ★★
Author(s): Reed
 satisfy
satisfy 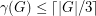 ?
? Keywords: cubic graph; domination
A generalization of Vizing's Theorem? ★★
Author(s): Rosenfeld
 be a simple
be a simple 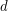 -uniform hypergraph, and assume that every set of
-uniform hypergraph, and assume that every set of 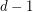 points is contained in at most
points is contained in at most  edges. Then there exists an
edges. Then there exists an 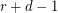 -edge-coloring so that any two edges which share
-edge-coloring so that any two edges which share 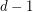 vertices have distinct colors.
vertices have distinct colors. Keywords: edge-coloring; hypergraph; Vizing
Distribution and upper bound of mimic numbers ★★
Author(s): Bhattacharyya
Let the notation 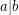 denote ''
denote '' divides
divides  ''. The mimic function in number theory is defined as follows [1].
''. The mimic function in number theory is defined as follows [1].
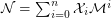 divisible by
divisible by 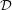 , the mimic function,
, the mimic function, 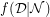 , is given by,
, is given by,
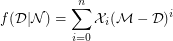
By using this definition of mimic function, the mimic number of any non-prime integer is defined as follows [1].
 is defined to be the mimic number of any positive integer
is defined to be the mimic number of any positive integer 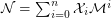 , with respect to
, with respect to 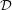 , for the minimum value of which
, for the minimum value of which 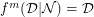 .
. Given these two definitions and a positive integer 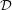 , find the distribution of mimic numbers of those numbers divisible by
, find the distribution of mimic numbers of those numbers divisible by 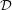 .
.
Again, find whether there is an upper bound of mimic numbers for a set of numbers divisible by any fixed positive integer 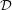 .
.
Keywords: Divisibility; mimic function; mimic number
Coloring random subgraphs ★★
Author(s): Bukh
If  is a graph and
is a graph and ![$ p \in [0,1] $](/files/tex/1d076f7332523eb59bd7deae19667f83f0a3b6e0.png) , we let
, we let 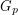 denote a subgraph of
denote a subgraph of  where each edge of
where each edge of  appears in
appears in 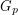 with independently with probability
with independently with probability 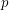 .
.
 so that
so that 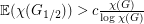 ?
? Keywords: coloring; random graph
Are vertex minor closed classes chi-bounded? ★★
Author(s): Geelen
Keywords: chi-bounded; circle graph; coloring; vertex minor
Graphs with a forbidden induced tree are chi-bounded ★★★
Author(s): Gyarfas
Say that a family 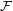 of graphs is
of graphs is 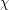 -bounded if there exists a function
-bounded if there exists a function 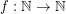 so that every
so that every 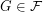 satisfies
satisfies 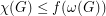 .
.
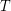 , the family of graphs with no induced subgraph isomorphic to
, the family of graphs with no induced subgraph isomorphic to 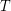 is
is 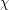 -bounded.
-bounded. Keywords: chi-bounded; coloring; excluded subgraph; tree
Asymptotic Distribution of Form of Polyhedra ★★
Author(s): Rüdinger
 edges. Define a form parameter for a polyhedron as
edges. Define a form parameter for a polyhedron as 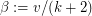 where
where  is the number of vertices. What is the distribution of
is the number of vertices. What is the distribution of 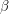 for
for 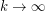 ?
? Keywords: polyhedral graphs, distribution
Domination in plane triangulations ★★
 has a dominating set of size
has a dominating set of size 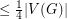 .
. Keywords: coloring; domination; multigrid; planar graph; triangulation
Erdös-Szekeres conjecture ★★★
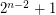 points in the plane in general position contains a subset of
points in the plane in general position contains a subset of  points which form a convex
points which form a convex  -gon.
-gon. Keywords: combinatorial geometry; Convex Polygons; ramsey theory
Inequality of the means ★★★
Author(s):
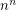 rectangular
rectangular  -dimensional boxes each of which has side lengths
-dimensional boxes each of which has side lengths 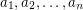 inside an
inside an  -dimensional cube with side length
-dimensional cube with side length 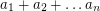 ?
? Keywords: arithmetic mean; geometric mean; Inequality; packing
P vs. PSPACE ★★★
Author(s): Folklore
Keywords: P; PSPACE; separation; unconditional
Sums of independent random variables with unbounded variance ★★
Author(s): Feige
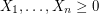 are independent random variables with
are independent random variables with ![$ \mathbb{E}[X_i] \leq \mu $](/files/tex/e0268221532981debea25e9446c8ee6f112e1881.png) , then
, then ![$$\mathrm{Pr} \left( \sum X_i - \mathbb{E} \left[ \sum X_i \right ] < \delta \mu \right) \geq \min \left ( (1 + \delta)^{-1} \delta, e^{-1} \right).$$](/files/tex/03dc1130142ee6fefcc33888e2fb6137211bf327.png)
Keywords: Inequality; Probability Theory; randomness in TCS
Grunbaum's Conjecture ★★★
Author(s): Grunbaum
 is a simple loopless triangulation of an orientable surface, then the dual of
is a simple loopless triangulation of an orientable surface, then the dual of  is 3-edge-colorable.
is 3-edge-colorable. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University