 login/create account
login/create account
Recent Activity
$C^r$ Stability Conjecture ★★★★
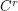 structurally stable diffeomorphism is hyperbolic.
structurally stable diffeomorphism is hyperbolic. Keywords: diffeomorphisms,; dynamical systems
Convex 'Fair' Partitions Of Convex Polygons ★★
Author(s): Nandakumar; Ramana
Basic Question: Given any positive integer n, can any convex polygon be partitioned into n convex pieces so that all pieces have the same area and same perimeter?
Definitions: Define a Fair Partition of a polygon as a partition of it into a finite number of pieces so that every piece has both the same area and the same perimeter. Further, if all the resulting pieces are convex, call it a Convex Fair Partition.
Questions: 1. (Rephrasing the above 'basic' question) Given any positive integer n, can any convex polygon be convex fair partitioned into n pieces?
2. If the answer to the above is "Not always'', how does one decide the possibility of such a partition for a given convex polygon and a given n? And if fair convex partition is allowed by a specific convex polygon for a give n, how does one find the optimal convex fair partition that minimizes the total length of the cut segments?
3. Finally, what could one say about higher dimensional analogs of this question?
Conjecture: The authors tend to believe that the answer to the above 'basic' question is "yes". In other words they guess: Every convex polygon allows a convex fair partition into n pieces for any n
Keywords: Convex Polygons; Partitioning
Growth of finitely presented groups ★★★
Author(s): Adyan
Keywords: finitely presented; growth
Ding's tau_r vs. tau conjecture ★★★
Author(s): Ding
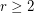 be an integer and let
be an integer and let  be a minor minimal clutter with
be a minor minimal clutter with 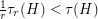 . Then either
. Then either  has a
has a 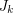 minor for some
minor for some 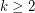 or
or  has Lehman's property.
has Lehman's property. Keywords: clutter; covering; MFMC property; packing
Equality in a matroidal circumference bound ★★
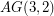 the only 3-connected matroid for which equality holds in the bound
the only 3-connected matroid for which equality holds in the bound 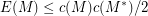 where
where 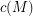 is the circumference (i.e. largest circuit size) of
is the circumference (i.e. largest circuit size) of 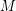 ?
? Keywords: circumference
Highly arc transitive two ended digraphs ★★
Author(s): Cameron; Praeger; Wormald
 is a highly arc transitive digraph with two ends, then every tile of
is a highly arc transitive digraph with two ends, then every tile of  is a disjoint union of complete bipartite graphs.
is a disjoint union of complete bipartite graphs. Keywords: arc transitive; digraph; infinite graph
Strong matchings and covers ★★★
Author(s): Aharoni
Let  be a hypergraph. A strongly maximal matching is a matching
be a hypergraph. A strongly maximal matching is a matching 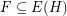 so that
so that 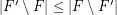 for every matching
for every matching 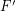 . A strongly minimal cover is a (vertex) cover
. A strongly minimal cover is a (vertex) cover 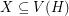 so that
so that 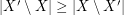 for every cover
for every cover 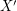 .
.
 is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size 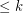 for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover. Keywords: cover; infinite graph; matching
Unfriendly partitions ★★★
If  is a graph, we say that a partition of
is a graph, we say that a partition of 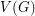 is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.
is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.
Keywords: coloring; infinite graph; partition
Universal highly arc transitive digraphs ★★★
Author(s): Cameron; Praeger; Wormald
An alternating walk in a digraph is a walk 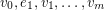 so that the vertex
so that the vertex  is either the head of both
is either the head of both 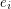 and
and 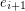 or the tail of both
or the tail of both 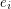 and
and 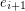 for every
for every  . A digraph is universal if for every pair of edges
. A digraph is universal if for every pair of edges 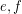 , there is an alternating walk containing both
, there is an alternating walk containing both  and
and 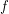
Keywords: arc transitive; digraph
P vs. NP ★★★★
Keywords: Complexity Class; Computational Complexity; Millenium Problems; NP; P; polynomial algorithm
F_d versus F_{d+1} ★★★
Author(s): Krajicek
 such that for any
such that for any 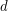 there is a sequence of tautologies of depth
there is a sequence of tautologies of depth  that have polynomial (or quasi-polynomial) size proofs in depth
that have polynomial (or quasi-polynomial) size proofs in depth 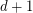 Frege system
Frege system 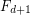 but requires exponential size
but requires exponential size 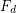 proofs.
proofs. Keywords: Frege system; short proof
Even vs. odd latin squares ★★★
A latin square is even if the product of the signs of all of the row and column permutations is 1 and is odd otherwise.
 , the number of even latin squares of order
, the number of even latin squares of order  and the number of odd latin squares of order
and the number of odd latin squares of order  are different.
are different. Keywords: latin square
Universal Steiner triple systems ★★
Author(s): Grannell; Griggs; Knor; Skoviera
Keywords: cubic graph; Steiner triple system
Monotone 4-term Arithmetic Progressions ★★
Author(s): Davis; Entringer; Graham; Simmons
Keywords: monotone arithmetic progression; permutation
The Bermond-Thomassen Conjecture ★★
 , every digraph with minimum out-degree at least
, every digraph with minimum out-degree at least 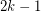 contains
contains  disjoint cycles.
disjoint cycles. Keywords: cycles
Continous analogue of Hirsch conjecture ★★
Author(s): Deza; Terlaky; Zinchenko
 inequalities in dimension
inequalities in dimension 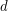 is
is  .
. Average diameter of a bounded cell of a simple arrangement ★★
Author(s): Deza; Terlaky; Zinchenko
 hyperplanes in dimension
hyperplanes in dimension 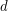 is not greater than
is not greater than 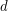 .
. Keywords: arrangement; diameter; polytope
Drawing disconnected graphs on surfaces ★★
Author(s): DeVos; Mohar; Samal
 be the disjoint union of the graphs
be the disjoint union of the graphs 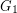 and
and 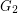 and let
and let 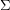 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 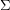 has the property that
has the property that 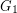 and
and 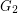 are disjoint?
are disjoint? Keywords: crossing number; surface
Matchings extend to Hamiltonian cycles in hypercubes ★★
Keywords: Hamiltonian cycle; hypercube; matching
Linear Hypergraphs with Dimension 3 ★★
Author(s): de Fraysseix; Ossona de Mendez; Rosenstiehl
Keywords: Hypergraphs

 Drupal
Drupal CSI of Charles University
CSI of Charles University