 login/create account
login/create account
Recent Activity
Tarski's exponential function problem ★★
Author(s): Tarski
Keywords: Decidability
Counting 3-colorings of the hex lattice ★★
Author(s): Thomassen
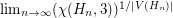 .
. Keywords: coloring; Lieb's Ice Constant; tiling; torus
Dense rational distance sets in the plane ★★★
Author(s): Ulam
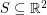 so that all pairwise distances between points in
so that all pairwise distances between points in 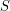 are rational?
are rational? Keywords: integral distance; rational distance
Negative association in uniform forests ★★
Author(s): Pemantle
 be a finite graph, let
be a finite graph, let 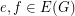 , and let
, and let 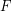 be the edge set of a forest chosen uniformly at random from all forests of
be the edge set of a forest chosen uniformly at random from all forests of  . Then
. Then ![\[ {\mathbb P}(e \in F \mid f \in F}) \le {\mathbb P}(e \in F) \]](/files/tex/1fe7ac9c579238670e3aa16ae401e8194e1c3da3.png)
Keywords: forest; negative association
Wall-Sun-Sun primes and Fibonacci divisibility ★★
Author(s):
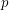 , there exists a Fibonacci number divisible by
, there exists a Fibonacci number divisible by 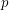 exactly once.
exactly once. Equivalently:
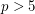 ,
, 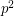 does not divide
does not divide 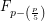 where
where 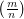 is the Legendre symbol.
is the Legendre symbol. Total Colouring Conjecture ★★★
Author(s): Behzad
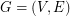 is an assignment of colors to the vertices and the edges of
is an assignment of colors to the vertices and the edges of  such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph
such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph  ,
, 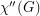 , equals the minimum number of colors needed in a total coloring of
, equals the minimum number of colors needed in a total coloring of  . It is an old conjecture of Behzad that for every graph
. It is an old conjecture of Behzad that for every graph  , the total chromatic number equals the maximum degree of a vertex in
, the total chromatic number equals the maximum degree of a vertex in  ,
, 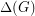 plus one or two. In other words,
plus one or two. In other words, ![\[\chi''(G)=\Delta(G)+1\ \ or \ \ \Delta(G)+2.\]](/files/tex/d4ea30e930ec20e02c5a03c6322e6d99a6bdb63a.png)
Keywords: Total coloring
Edge Reconstruction Conjecture ★★★
Author(s): Harary
Every simple graph with at least 4 edges is reconstructible from it's edge deleted subgraphs
Keywords: reconstruction
Nearly spanning regular subgraphs ★★★
 and every positive integer
and every positive integer  , there exists
, there exists  so that every simple
so that every simple  -regular graph
-regular graph  with
with 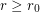 has a
has a  -regular subgraph
-regular subgraph  with
with 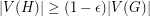 .
. Degenerate colorings of planar graphs ★★★
Author(s): Borodin
A graph  is
is  -degenerate if every subgraph of
-degenerate if every subgraph of  has a vertex of degree
has a vertex of degree 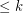 .
.
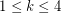 , the union of any
, the union of any  color classes induces a
color classes induces a 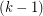 -degenerate graph.
-degenerate graph. Keywords: coloring; degenerate; planar
Partial List Coloring ★★★
Author(s): Iradmusa
Let  be a simple graph, and for every list assignment
be a simple graph, and for every list assignment 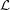 let
let 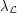 be the maximum number of vertices of
be the maximum number of vertices of  which are colorable with respect to
which are colorable with respect to 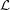 . Define
. Define  , where the minimum is taken over all list assignments
, where the minimum is taken over all list assignments 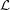 with
with 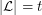 for all
for all 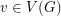 .
.
 be a graph with list chromatic number
be a graph with list chromatic number 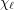 and
and 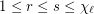 . Then
. Then ![\[\frac{\lambda_r}{r}\geq\frac{\lambda_s}{s}.\]](/files/tex/47be18e956355dd433b88b66eabf01a9e3ed5f61.png)
Keywords: list assignment; list coloring
Cube-Simplex conjecture ★★★
Author(s): Kalai
 , there exists an integer
, there exists an integer 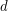 so that every polytope of dimension
so that every polytope of dimension 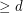 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube. Partial List Coloring ★★★
Author(s): Albertson; Grossman; Haas
 be a simple graph with
be a simple graph with  vertices and list chromatic number
vertices and list chromatic number 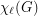 . Suppose that
. Suppose that 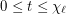 and each vertex of
and each vertex of  is assigned a list of
is assigned a list of 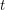 colors. Then at least
colors. Then at least 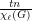 vertices of
vertices of  can be colored from these lists.
can be colored from these lists. Keywords: list assignment; list coloring
Combinatorial covering designs ★
Author(s): Gordon; Mills; Rödl; Schönheim
A 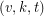 covering design, or covering, is a family of
covering design, or covering, is a family of  -subsets, called blocks, chosen from a
-subsets, called blocks, chosen from a  -set, such that each
-set, such that each 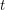 -subset is contained in at least one of the blocks. The number of blocks is the covering’s size, and the minimum size of such a covering is denoted by
-subset is contained in at least one of the blocks. The number of blocks is the covering’s size, and the minimum size of such a covering is denoted by 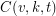 .
.
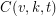 . Find a procedure for constructing minimal coverings.
. Find a procedure for constructing minimal coverings. Keywords: recreational mathematics
Burnside problem ★★★★
Author(s): Burnside
 generators and exponent
generators and exponent  , is it necessarily finite?
, is it necessarily finite? Keywords:
Laplacian Degrees of a Graph ★★
Author(s): Guo
 is a connected graph on
is a connected graph on  vertices, then
vertices, then 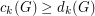 for
for 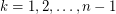 .
. Keywords: degree sequence; Laplacian matrix
Random stable roommates ★★
Author(s): Mertens
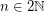 people admits a solution is
people admits a solution is 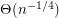 .
. Keywords: stable marriage; stable roommates
Chowla's cosine problem ★★★
Author(s): Chowla
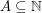 be a set of
be a set of  positive integers and set
positive integers and set ![\[m(A) = - \min_x \sum_{a \in A} \cos(ax).\]](/files/tex/7a772ebd0b7fd98eeab7fda3a5e9674b1dc4c984.png) What is
What is  ?
? Keywords: circle; cosine polynomial
End-Devouring Rays ★
Author(s): Georgakopoulos
 be a graph,
be a graph,  a countable end of
a countable end of  , and
, and 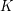 an infinite set of pairwise disjoint
an infinite set of pairwise disjoint  -rays in
-rays in  . Prove that there is a set
. Prove that there is a set 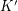 of pairwise disjoint
of pairwise disjoint  -rays that devours
-rays that devours  such that the set of starting vertices of rays in
such that the set of starting vertices of rays in 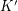 equals the set of starting vertices of rays in
equals the set of starting vertices of rays in 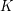 .
. Seagull problem ★★★
Author(s): Seymour
 vertex graph with no independent set of size
vertex graph with no independent set of size 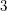 has a complete graph on
has a complete graph on 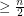 vertices as a minor.
vertices as a minor. Keywords: coloring; complete graph; minor

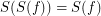 for every endo-
for every endo-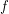 ?
?  Drupal
Drupal CSI of Charles University
CSI of Charles University