 login/create account
login/create account
Recent Activity
Transversal achievement game on a square grid ★★
Author(s): Erickson
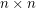 grid. The first player (if any) to occupy a set of
grid. The first player (if any) to occupy a set of  cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play?
cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play? Keywords: game
Graceful Tree Conjecture ★★★
Author(s):
Keywords: combinatorics; graceful labeling
Extremal problem on the number of tree endomorphism ★★
Author(s): Zhicong Lin
 vertices' trees, the star with
vertices' trees, the star with  vertices has the most endomorphisms, while the path with
vertices has the most endomorphisms, while the path with  vertices has the least endomorphisms.
vertices has the least endomorphisms. Keywords:
3-Colourability of Arrangements of Great Circles ★★
Author(s): Felsner; Hurtado; Noy; Streinu
Consider a set 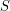 of great circles on a sphere with no three circles meeting at a point. The arrangement graph of
of great circles on a sphere with no three circles meeting at a point. The arrangement graph of 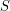 has a vertex for each intersection point, and an edge for each arc directly connecting two intersection points. So this arrangement graph is 4-regular and planar.
has a vertex for each intersection point, and an edge for each arc directly connecting two intersection points. So this arrangement graph is 4-regular and planar.
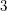 -colourable.
-colourable. Keywords: arrangement graph; graph coloring
KPZ Universality Conjecture ★★★
Author(s):
Keywords: KPZ equation, central limit theorem
Friendly partitions ★★
Author(s): DeVos
A friendly partition of a graph is a partition of the vertices into two sets so that every vertex has at least as many neighbours in its own class as in the other.
 , all but finitely many
, all but finitely many  -regular graphs have friendly partitions?
-regular graphs have friendly partitions? Finite entailment of Positive Horn logic ★★
Author(s): Martin
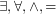 . Does the fragment
. Does the fragment 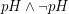 have the finite model property?
have the finite model property? Keywords: entailment; finite satisfiability; horn logic
Triangle free strongly regular graphs ★★★
Author(s):
Keywords: strongly regular; triangle free
A discrete iteration related to Pierce expansions ★★
Author(s): Shallit
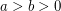 be integers. Set
be integers. Set 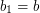 and
and 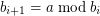 for
for 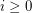 . Eventually we have
. Eventually we have 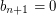 ; put
; put 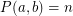 .
.
Example: 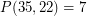 , since
, since 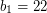 ,
, 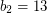 ,
, 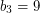 ,
, 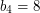 ,
, 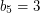 ,
, 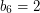 ,
, 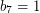 ,
, 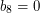 .
.
Prove or disprove: 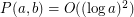 .
.
Keywords: Pierce expansions
Bounding the chromatic number of triangle-free graphs with fixed maximum degree ★★
 has chromatic number at most
has chromatic number at most 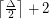 .
.
Keywords: chromatic number; girth; maximum degree; triangle free
Hedetniemi's Conjecture ★★★
Author(s): Hedetniemi
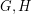 are simple finite graphs, then
are simple finite graphs, then  .
. Here 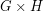 is the tensor product (also called the direct or categorical product) of
is the tensor product (also called the direct or categorical product) of  and
and  .
.
Keywords: categorical product; coloring; homomorphism; tensor product
Diophantine quintuple conjecture ★★
Author(s):
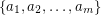 is called a Diophantine
is called a Diophantine  -tuple if
-tuple if 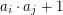 is a perfect square for all
is a perfect square for all 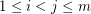 .
. It would follow from the following stronger conjecture [Da]:
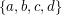 is a Diophantine quadruple and
is a Diophantine quadruple and 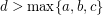 , then
, then 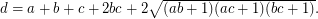
Keywords:
Several ways to apply a (multivalued) multiargument function to a family of filters ★★★
Author(s): Porton
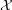 be an indexed family of filters on sets. Which of the below items are always pairwise equal?
be an indexed family of filters on sets. Which of the below items are always pairwise equal?
1. The funcoid corresponding to this function (considered as a single argument function on indexed families) applied to the reloidal product of filters 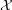 .
.
2. The funcoid corresponding to this function (considered as a single argument function on indexed families) applied to the starred reloidal product of filters 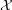 .
.
3. 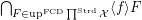 .
.
Keywords: funcoid; function; multifuncoid; staroid
Jones' conjecture ★★
For a graph  , let
, let 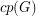 denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let
denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let 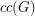 denote the cardinality of a minimum feedback vertex set (set of vertices
denote the cardinality of a minimum feedback vertex set (set of vertices 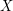 so that
so that 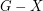 is acyclic).
is acyclic).
 ,
, 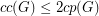 .
. Keywords: cycle packing; feedback vertex set; planar graph
Multicolour Erdős--Hajnal Conjecture ★★★
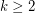 and fixed colouring
and fixed colouring 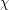 of
of 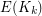 with
with  colours, there exists
colours, there exists 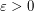 such that every colouring of the edges of
such that every colouring of the edges of 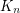 contains either
contains either  vertices whose edges are coloured according to
vertices whose edges are coloured according to 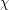 or
or 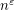 vertices whose edges are coloured with at most
vertices whose edges are coloured with at most 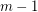 colours.
colours. Keywords: ramsey theory
Sidorenko's Conjecture ★★★
Author(s): Sidorenko
 and graph
and graph  , the number of homomorphisms from
, the number of homomorphisms from  to
to  is at least
is at least 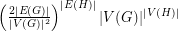 .
. Keywords: density problems; extremal combinatorics; homomorphism
Edge-Unfolding Convex Polyhedra ★★
Author(s): Shephard
Point sets with no empty pentagon ★
Author(s): Wood
Keywords: combinatorial geometry; visibility graph
Singmaster's conjecture ★★
Author(s): Singmaster
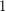 .
. The number 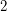 appears once in Pascal's triangle,
appears once in Pascal's triangle, 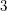 appears twice,
appears twice,  appears three times, and
appears three times, and 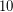 appears
appears 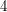 times. There are infinite families of numbers known to appear
times. There are infinite families of numbers known to appear  times. The only number known to appear
times. The only number known to appear 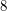 times is
times is 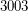 . It is not known whether any number appears more than
. It is not known whether any number appears more than 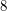 times. The conjectured upper bound could be
times. The conjectured upper bound could be 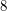 ; Singmaster thought it might be
; Singmaster thought it might be 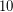 or
or 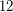 . See Singmaster's conjecture.
. See Singmaster's conjecture.
Keywords: Pascal's triangle
Waring rank of determinant ★★
Author(s): Teitler
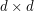 generic matrix?
generic matrix? For simplicity say we work over the complex numbers. The 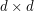 generic matrix is the matrix with entries
generic matrix is the matrix with entries 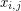 for
for 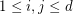 . Its determinant is a homogeneous form of degree
. Its determinant is a homogeneous form of degree 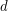 , in
, in 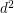 variables. If
variables. If 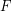 is a homogeneous form of degree
is a homogeneous form of degree 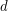 , a power sum expression for
, a power sum expression for 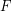 is an expression of the form
is an expression of the form 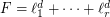 , the
, the 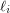 (homogeneous) linear forms. The Waring rank of
(homogeneous) linear forms. The Waring rank of 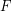 is the least number of terms
is the least number of terms  in any power sum expression for
in any power sum expression for 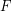 . For example, the expression
. For example, the expression 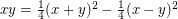 means that
means that 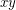 has Waring rank
has Waring rank 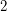 (it can't be less than
(it can't be less than 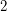 , as
, as 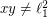 ).
).
The 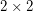 generic determinant
generic determinant 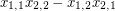 (or
(or 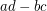 ) has Waring rank
) has Waring rank 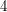 . The Waring rank of the
. The Waring rank of the 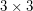 generic determinant is at least
generic determinant is at least 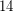 and no more than
and no more than 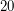 , see for instance Lower bound for ranks of invariant forms, Example 4.1. The Waring rank of the permanent is also of interest. The comparison between the determinant and permanent is potentially relevant to Valiant's "VP versus VNP" problem.
, see for instance Lower bound for ranks of invariant forms, Example 4.1. The Waring rank of the permanent is also of interest. The comparison between the determinant and permanent is potentially relevant to Valiant's "VP versus VNP" problem.
Keywords: Waring rank, determinant

 Drupal
Drupal CSI of Charles University
CSI of Charles University