 login/create account
login/create account
Recent Activity
Reed's omega, delta, and chi conjecture ★★★
Author(s): Reed
For a graph  , we define
, we define 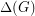 to be the maximum degree,
to be the maximum degree, 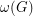 to be the size of the largest clique subgraph, and
to be the size of the largest clique subgraph, and 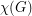 to be the chromatic number of
to be the chromatic number of  .
.
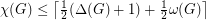 for every graph
for every graph  .
. Keywords: coloring
Pebbling a cartesian product ★★★
Author(s): Graham
We let 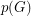 denote the pebbling number of a graph
denote the pebbling number of a graph  .
.
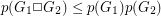 .
. Rendezvous on a line ★★★
Author(s): Alpern
 (first time when the players occupy the same point) which can be achieved assuming the two players must adopt the same strategy?
(first time when the players occupy the same point) which can be achieved assuming the two players must adopt the same strategy? Keywords: game theory; optimization; rendezvous
Linial-Berge path partition duality ★★★
 -norm of a path partition on a directed graph
-norm of a path partition on a directed graph  is no more than the maximal size of an induced
is no more than the maximal size of an induced  -colorable subgraph.
-colorable subgraph. Keywords: coloring; directed path; partition
What is the smallest number of disjoint spanning trees made a graph Hamiltonian ★★
Author(s): Goldengorin
We are given a complete simple undirected weighted graph 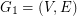 and its first arbitrary shortest spanning tree
and its first arbitrary shortest spanning tree 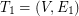 . We define the next graph
. We define the next graph 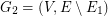 and find on
and find on 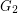 the second arbitrary shortest spanning tree
the second arbitrary shortest spanning tree 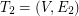 . We continue similarly by finding
. We continue similarly by finding 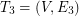 on
on 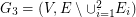 , etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let
, etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let 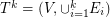 be the graph obtained as union of all
be the graph obtained as union of all  disjoint trees.
disjoint trees.
Question 1. What is the smallest number of disjoint spanning trees creates a graph 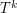 containing a Hamiltonian path.
containing a Hamiltonian path.
Question 2. What is the smallest number of disjoint spanning trees creates a graph 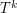 containing a shortest Hamiltonian path?
containing a shortest Hamiltonian path?
Questions 3 and 4. Replace in questions 1 and 2 a shortest spanning tree by a 1-tree. What is the smallest number of disjoint 1-trees creates a Hamiltonian graph? What is the smallest number of disjoint 1-trees creates a graph containing a shortest Hamiltonian cycle?
Keywords: 1-trees; cycle; Hamitonian path; spanning trees
Davenport's constant ★★★
Author(s):
For a finite (additive) abelian group  , the Davenport constant of
, the Davenport constant of  , denoted
, denoted 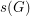 , is the smallest integer
, is the smallest integer 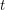 so that every sequence of elements of
so that every sequence of elements of  with length
with length 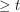 has a nontrivial subsequence which sums to zero.
has a nontrivial subsequence which sums to zero.
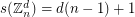
Keywords: Davenport constant; subsequence sum; zero sum
Coloring and immersion ★★★
Author(s): Abu-Khzam; Langston
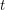 , every (loopless) graph
, every (loopless) graph  with
with 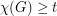 immerses
immerses 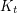 .
. Keywords: coloring; complete graph; immersion
Rainbow AP(4) in an almost equinumerous coloring ★★
Author(s): Conlon
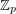 , for
, for 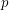 a large prime, always contain a rainbow
a large prime, always contain a rainbow 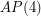 if each of the color classes is of size of either
if each of the color classes is of size of either 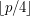 or
or 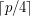 ?
? Keywords: arithmetic progression; rainbow
The intersection of two perfect matchings ★★
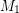 ,
, 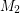 so that
so that 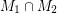 does not contain an odd edge-cut.
does not contain an odd edge-cut. Keywords: cubic; nowhere-zero flow; perfect matching
Counterexamples to the Baillie-PSW primality test ★★
Author(s):
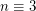 or
or 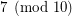 which divides both
which divides both 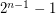 (see Fermat pseudoprime) and the Fibonacci number
(see Fermat pseudoprime) and the Fibonacci number 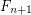 (see Lucas pseudoprime), or prove that there is no such
(see Lucas pseudoprime), or prove that there is no such  .
. Keywords:
A sextic counterexample to Euler's sum of powers conjecture ★★
Author(s): Euler
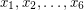 such that
such that 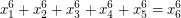 or prove that such integers do not exist.
or prove that such integers do not exist. Keywords:
Geodesic cycles and Tutte's Theorem ★★
Author(s): Georgakopoulos; Sprüssel
 is a
is a 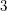 -connected finite graph, is there an assignment of lengths
-connected finite graph, is there an assignment of lengths 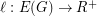 to the edges of
to the edges of  , such that every
, such that every 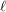 -geodesic cycle is peripheral?
-geodesic cycle is peripheral? Keywords: cycle space; geodesic cycles; peripheral cycles
Oriented chromatic number of planar graphs ★★
Author(s):
An oriented colouring of an oriented graph is assignment  of colours to the vertices such that no two arcs receive ordered pairs of colours
of colours to the vertices such that no two arcs receive ordered pairs of colours 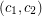 and
and 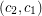 . It is equivalent to a homomorphism of the digraph onto some tournament of order
. It is equivalent to a homomorphism of the digraph onto some tournament of order  .
.
Keywords: oriented coloring; oriented graph; planar graph
Covering systems with big moduli ★★
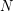 exist a covering system with all moduli distinct and at least equal to~
exist a covering system with all moduli distinct and at least equal to~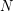 ?
? Keywords: covering system
Odd incongruent covering systems ★★★
Keywords: covering system
Hamiltonian cycles in powers of infinite graphs ★★
Author(s): Georgakopoulos
- \item If
 is a countable connected graph then its third power is hamiltonian. \item If
is a countable connected graph then its third power is hamiltonian. \item If  is a 2-connected countable graph then its square is hamiltonian.
is a 2-connected countable graph then its square is hamiltonian. Keywords: hamiltonian; infinite graph
Hamiltonian cycles in line graphs of infinite graphs ★★
Author(s): Georgakopoulos
- \item If
 is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph
is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph 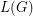 of a locally finite graph
of a locally finite graph  is 4-connected, then
is 4-connected, then 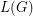 is hamiltonian.
is hamiltonian. Keywords: hamiltonian; infinite graph; line graphs
Hamiltonian cycles in line graphs ★★★
Author(s): Thomassen
Keywords: hamiltonian; line graphs
Infinite uniquely hamiltonian graphs ★★
Author(s): Mohar
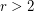 ?
? Keywords: hamiltonian; infinite graph; uniquely hamiltonian
Linear-size circuits for stable $0,1 < 2$ sorting? ★★
Author(s): Regan
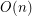 -size circuits compute the function
-size circuits compute the function 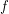 on
on 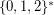 defined inductively by
defined inductively by 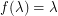 ,
, 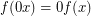 ,
, 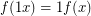 , and
, and 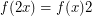 ?
? 
 Drupal
Drupal CSI of Charles University
CSI of Charles University