 login/create account
login/create account
Recent Activity
Universal point sets for planar graphs ★★★
Author(s): Mohar
We say that a set 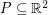 is
is  -universal if every
-universal if every  vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in
vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in 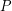 , and all edges are (non-intersecting) straight line segments.
, and all edges are (non-intersecting) straight line segments.
 -universal set of size
-universal set of size 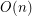 ?
? Keywords: geometric graph; planar graph; universal set
Antichains in the cycle continuous order ★★
Author(s): DeVos
If  ,
, are graphs, a function
are graphs, a function 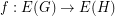 is called cycle-continuous if the pre-image of every element of the (binary) cycle space of
is called cycle-continuous if the pre-image of every element of the (binary) cycle space of  is a member of the cycle space of
is a member of the cycle space of  .
.
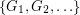 so that there is no cycle continuous mapping between
so that there is no cycle continuous mapping between 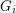 and
and 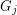 whenever
whenever 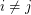 ?
? Fat 4-polytopes ★★★
Author(s): Eppstein; Kuperberg; Ziegler
The fatness of a 4-polytope 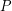 is defined to be
is defined to be 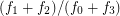 where
where 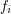 is the number of faces of
is the number of faces of 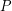 of dimension
of dimension 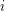 .
.
 so that every convex 4-polytope has fatness at most
so that every convex 4-polytope has fatness at most  ?
? The Crossing Number of the Complete Bipartite Graph ★★★
Author(s): Turan
The crossing number 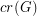 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
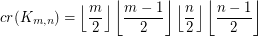
Keywords: complete bipartite graph; crossing number
Woodall's Conjecture ★★★
Author(s): Woodall
 is a directed graph with smallest directed cut of size
is a directed graph with smallest directed cut of size  , then
, then  has
has  disjoint dijoins.
disjoint dijoins. Pentagon problem ★★★
Author(s): Nesetril
 be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than 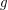 . Is it true that for large enough~
. Is it true that for large enough~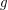 there is a homomorphism
there is a homomorphism 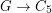 ?
? Keywords: cubic; homomorphism
Ryser's conjecture ★★★
Author(s): Ryser
 be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 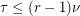 .
. Keywords: hypergraph; matching; packing
The Erdös-Hajnal Conjecture ★★★
 , there exists a constant
, there exists a constant 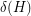 , so that every graph
, so that every graph  without an induced subgraph isomorphic to
without an induced subgraph isomorphic to  contains either a clique or an independent set of size
contains either a clique or an independent set of size 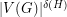 .
. Keywords: induced subgraph
Hamiltonian paths and cycles in vertex transitive graphs ★★★
Author(s): Lovasz
Keywords: cycle; hamiltonian; path; vertex-transitive
57-regular Moore graph? ★★★
Keywords: cage; Moore graph
Few subsequence sums in Z_n x Z_n ★★
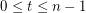 , the sequence in
, the sequence in 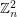 consisting of
consisting of 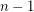 copes of
copes of 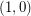 and
and 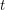 copies of
copies of 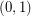 has the fewest number of distinct subsequence sums over all zero-free sequences from
has the fewest number of distinct subsequence sums over all zero-free sequences from 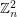 of length
of length 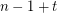 .
. Keywords: subsequence sum; zero sum
Olson's Conjecture ★★
Author(s): Olson
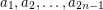 is a sequence of elements from a multiplicative group of order
is a sequence of elements from a multiplicative group of order  , then there exist
, then there exist 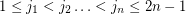 so that
so that 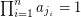 .
. Keywords: zero sum
Highly connected graphs with no K_n minor ★★★
Author(s): Thomas
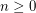 , that every sufficiently large
, that every sufficiently large  -connected graph without a
-connected graph without a 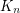 minor has a set of
minor has a set of 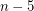 vertices whose deletion results in a planar graph?
vertices whose deletion results in a planar graph? Keywords: connectivity; minor
The Alon-Tarsi basis conjecture ★★
Author(s): Alon; Linial; Meshulam
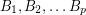 are invertible
are invertible 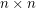 matrices with entries in
matrices with entries in 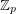 for a prime
for a prime 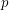 , then there is a
, then there is a 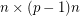 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base. Keywords: additive basis; matrix
The permanent conjecture ★★
Author(s): Kahn
 is an invertible
is an invertible 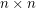 matrix, then there is an
matrix, then there is an 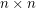 submatrix
submatrix 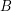 of
of ![$ [A A] $](/files/tex/d1e9d82c656535b507686183e640178057fae455.png) so that
so that 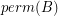 is nonzero.
is nonzero. Keywords: invertible; matrix; permanent
The additive basis conjecture ★★★
Author(s): Jaeger; Linial; Payan; Tarsi
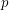 , there is a constant
, there is a constant 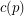 (possibly
(possibly 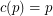 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 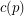 bases of the vector space
bases of the vector space 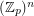 contains an additive basis.
contains an additive basis. Keywords: additive basis; matrix
A nowhere-zero point in a linear mapping ★★★
Author(s): Jaeger
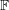 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 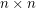 matrix with entries in
matrix with entries in 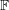 , then there are column vectors
, then there are column vectors 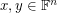 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 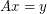 .
. Keywords: invertible; nowhere-zero flow
Partitioning edge-connectivity ★★
Author(s): DeVos
 be an
be an 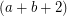 -edge-connected graph. Does there exist a partition
-edge-connected graph. Does there exist a partition 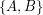 of
of 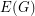 so that
so that 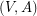 is
is  -edge-connected and
-edge-connected and 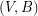 is
is  -edge-connected?
-edge-connected? Keywords: edge-coloring; edge-connectivity
Acyclic edge-colouring ★★
Author(s): Fiamcik
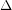 has a proper
has a proper 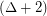 -edge-colouring so that every cycle contains edges of at least three distinct colours.
-edge-colouring so that every cycle contains edges of at least three distinct colours. Keywords: edge-coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University